斜率的概念、几何意义及其广泛应用
在数学和物理学领域,斜率是一个极其重要的概念。斜率,简单来说,指的是一条直线在平面直角坐标系中相对于横坐标的倾斜程度。
从几何意义上讲,斜率表示了直线上两点纵坐标的变化量与横坐标的变化量的比值。如果直线上有两点 A(x?, y?) 和 B(x?, y?),那么斜率 k 可以通过公式 k = (y? - y?) / (x? - x?) 来计算。
斜率的值具有明确的意义。当斜率为正数时,直线从左向右上升;斜率为负数时,直线从左向右下降;斜率为零,直线水平;斜率不存在时,直线垂直。
在数学中,斜率有着广泛的应用。在函数图像中,一次函数 y = kx + b 的斜率 k 决定了函数的增减性。对于二次函数的图像,其切线的斜率可以帮助我们分析函数的极值和单调性等性质。
在物理学中,斜率的应用也十分常见。例如在运动学中,位移-时间图像的斜率表示物体的速度;速度-时间图像的斜率则表示物体的加速度。
下面通过一个表格来更清晰地展示斜率在不同情境下的应用:
学科领域 具体应用 示例 数学 函数图像分析 一次函数的增减性判断 物理学 运动学分析 位移-时间图像中求速度总之,斜率作为一个基础且关键的概念,无论是在数学的理论研究还是物理学的实际应用中,都发挥着不可或缺的作用。它帮助我们更深入地理解和解决各种问题,为进一步的研究和实践提供了有力的工具。
【免责声明】本文仅代表作者本人观点,与和讯网无关。和讯网站对文中陈述、观点判断保持中立,不对所包含内容的准确性、可靠性或完整性提供任何明示或暗示的保证。请读者仅作参考,并请自行承担全部责任。邮箱:news_center@staff.hexun.com




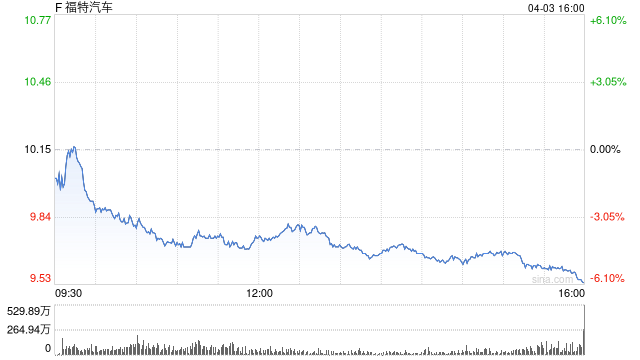

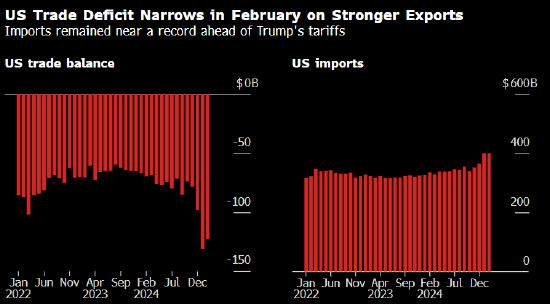

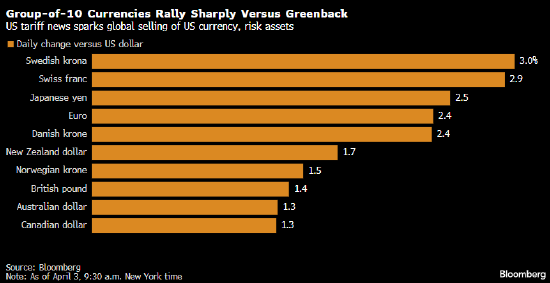






发表评论